20 Actividades Matemáticas Para Desarrollar El Pensamiento Lógico De: El pensamiento lógico-matemático, piedra angular del desarrollo cognitivo, se presenta aquí como un desafío apasionante. Este compendio de actividades, cuidadosamente diseñadas para diferentes grupos etarios – desde la primaria hasta la adolescencia – no solo busca el dominio de conceptos matemáticos, sino la cultivación de un razonamiento crítico y la resolución creativa de problemas.
Descubra cómo las matemáticas, lejos de ser una materia árida, se transforman en un fascinante juego intelectual que potencia la agilidad mental y el ingenio. Prepárese para un viaje enriquecedor a través de juegos de mesa, secuencias numéricas, acertijos lógicos y problemas geométricos que estimularán la mente de jóvenes curiosos y ávidos de conocimiento. Una aventura intelectual que comienza ahora mismo.
El presente documento explora la profunda interconexión entre las matemáticas y el desarrollo del pensamiento lógico. Se presentarán veinte actividades prácticas, categorizadas por nivel educativo, que buscan fomentar la resolución de problemas, el razonamiento deductivo, el pensamiento crítico y la creatividad. Cada actividad ha sido concebida para estimular diferentes aspectos del pensamiento lógico-matemático, desde el conteo y las secuencias en la etapa primaria, hasta la resolución de ecuaciones y la lógica proposicional en la secundaria y la adolescencia.
El enfoque se centra en la aplicación práctica del conocimiento matemático, convirtiendo el aprendizaje en una experiencia atractiva y estimulante.
El Pensamiento Lógico-Matemático: Un Pilar Fundamental en el Desarrollo Infantil: 20 Actividades Matemáticas Para Desarrollar El Pensamiento Lógico De
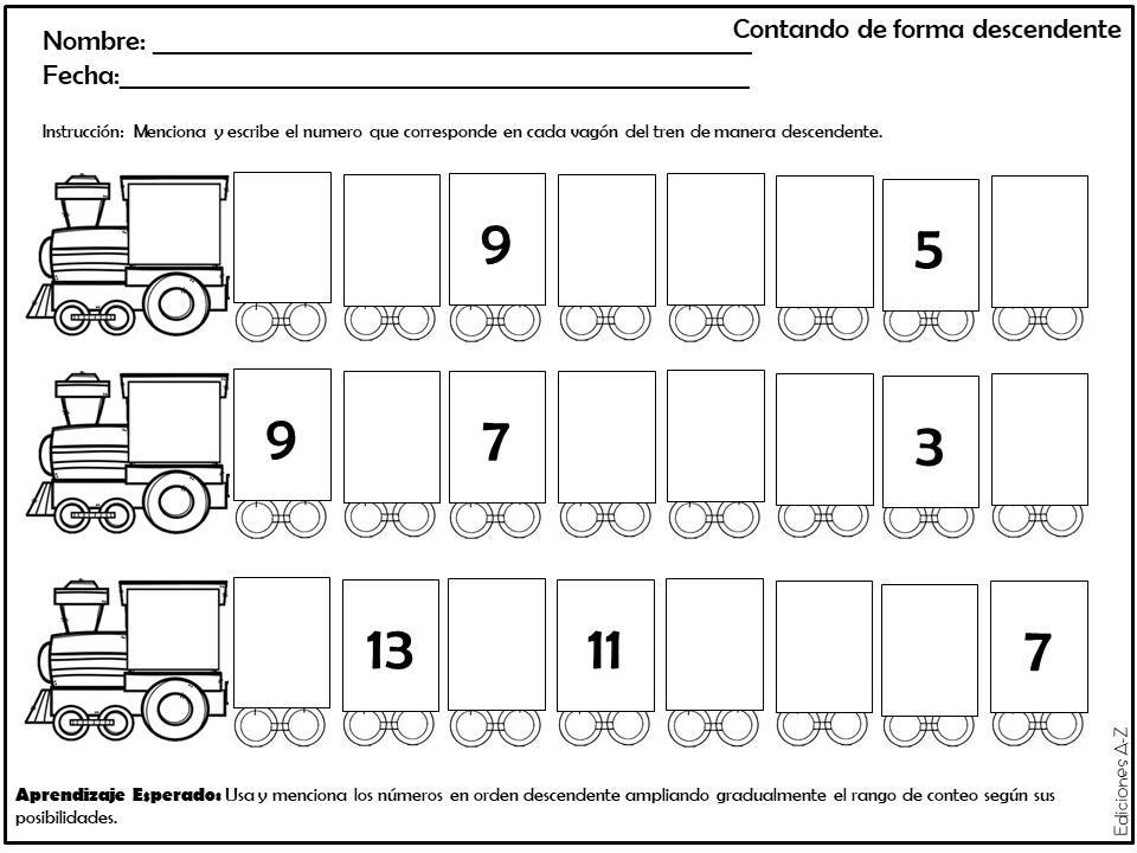
El desarrollo del pensamiento lógico-matemático es crucial para el crecimiento cognitivo de niños y jóvenes. Esta habilidad, intrínsecamente ligada a las matemáticas, facilita la resolución de problemas, el razonamiento crítico, y la toma de decisiones informadas a lo largo de la vida. La capacidad de analizar información, identificar patrones, y deducir conclusiones lógicas son pilares del éxito académico y personal.
Entender la relación intrínseca entre las matemáticas y el pensamiento lógico es fundamental para diseñar estrategias educativas efectivas.
El pensamiento lógico-matemático se define como la capacidad de razonar, analizar y resolver problemas utilizando conceptos y procedimientos matemáticos. Implica la habilidad de comprender relaciones, secuencias, y patrones; de formular hipótesis y probarlas; y de extraer conclusiones válidas a partir de la información disponible. Es un proceso dinámico que se construye gradualmente a través de la experiencia y la práctica.
Actividades para Niños de Primaria (6-8 Años)
En esta etapa, el aprendizaje se basa en la manipulación de objetos concretos y juegos lúdicos que estimulen la curiosidad y el razonamiento. Las actividades deben ser atractivas, sencillas y progresivas, enfatizando la comprensión conceptual sobre la memorización.
- Juego de Mesa: “La Carrera de las Sumas”: Un tablero con casillas numeradas, dados y fichas. Cada jugador lanza los dados, suma los resultados y avanza su ficha la cantidad de casillas correspondiente. El primero en llegar a la meta gana. Se pueden incorporar restas en niveles más avanzados.
- Juego de Mesa: “Construyendo Secuencias”: Se utilizan fichas con imágenes o números para formar secuencias lógicas. Los jugadores deben identificar el patrón y continuar la secuencia. La complejidad de las secuencias puede ajustarse según el nivel de los participantes.
- Juego de Mesa: “El Rompecabezas Matemático”: Se utilizan piezas de rompecabezas con números o operaciones matemáticas. Los jugadores deben ensamblar las piezas para formar una ecuación o una secuencia correcta. Este juego fomenta la resolución de problemas y el razonamiento espacial.
| Actividad | Descripción | Habilidad | Materiales |
|---|---|---|---|
| Conteo de objetos | Contar objetos cotidianos (juguetes, dulces, etc.) | Conteo, correspondencia uno a uno | Objetos cotidianos |
| Secuencias numéricas | Identificar y completar secuencias numéricas sencillas (1, 2, 3…) | Reconocimiento de patrones, secuencias | Tarjetas con números |
| Patrones con bloques | Crear patrones con bloques de colores o formas | Pensamiento espacial, patrones | Bloques de construcción |
| Juegos de memoria numérica | Memorizar y emparejar tarjetas con números | Memoria, reconocimiento numérico | Tarjetas con números |
| Creación de secuencias con imágenes | Crear secuencias con imágenes que representen una historia o acción | Secuencias, narración | Imágenes recortadas |
Actividad con Material Concreto: Suma y Resta con Bloques: Utilizando bloques de construcción, los niños pueden representar sumas y restas de forma visual y manipulativa. Por ejemplo, para representar 3 + 2, se colocan 3 bloques y luego se añaden 2 más, contando el total. Para la resta, se realiza el proceso inverso.
Actividades para Niños de Secundaria (9-12 Años)
En esta etapa, se puede introducir un nivel de abstracción mayor, utilizando problemas que requieren un razonamiento deductivo más complejo y la aplicación de estrategias de resolución de problemas.
- Problema 1: Tres amigos, Ana, Juan y Pedro, tienen diferentes edades. Ana es mayor que Juan, pero menor que Pedro. ¿Quién es el mayor?
- Problema 2: Un tren viaja a 60 km/h y otro a 80 km/h. Si ambos parten del mismo punto en direcciones opuestas, ¿a qué distancia estarán uno del otro después de 2 horas?
- Problema 3: Si todos los gatos son felinos y algunos felinos son salvajes, ¿todos los gatos son salvajes?
- Problema 4: Cinco casas de diferentes colores están situadas en una calle. En cada casa vive una persona de una nacionalidad diferente. Cada persona bebe una bebida diferente, fuma una marca de cigarrillos diferente y tiene una mascota diferente. Utilizando una serie de pistas, determinar qué mascota tiene cada persona.
- Problema 5: Un acertijo lógico que involucre la deducción de una secuencia de eventos a partir de pistas.
Creación de Secuencias Numéricas y Geométricas: Se puede iniciar con secuencias sencillas, como 2, 4, 6, 8… y luego ir aumentando la complejidad, introduciendo secuencias geométricas (3, 6, 12, 24…) o secuencias que combinen patrones numéricos y geométricos. El proceso debe incluir la identificación del patrón, la formulación de la regla y la predicción de los siguientes términos.
Juegos de Estrategia: Juegos como el ajedrez o las damas promueven el pensamiento estratégico, la planificación anticipada, y la evaluación de consecuencias. Analizar las jugadas del oponente y planificar las propias requiere un alto nivel de razonamiento lógico-matemático.
Actividades para Adolescentes (13-17 Años)
En esta etapa, se pueden abordar temas más complejos, requiriendo un mayor nivel de abstracción y la aplicación de conceptos matemáticos más avanzados.
Resolución de Problemas con Ecuaciones Lineales: Se pueden plantear problemas de la vida real que requieran la formulación y resolución de ecuaciones lineales. Por ejemplo, calcular el precio de un artículo con descuento o determinar la velocidad de un objeto en movimiento.
Juego de Ingenio con Lógica Proposicional: Se puede diseñar un juego que involucre la utilización de conectivos lógicos (y, o, no, si… entonces) para resolver acertijos o desafíos. Este tipo de juego fortalece la capacidad de razonamiento deductivo y la comprensión de la lógica simbólica.
Geometría y Razonamiento Espacial: Se pueden plantear problemas de geometría que requieran la visualización espacial y la aplicación de teoremas geométricos para resolver problemas. Por ejemplo, calcular el área o el volumen de figuras geométricas complejas.
| Problema | Descripción | Concepto Geométrico | Solución |
|---|---|---|---|
| Cálculo de área | Calcular el área de un terreno irregular. | Descomposición de figuras, cálculo de áreas | Dividir el terreno en figuras regulares y sumar sus áreas. |
| Volumen de un prisma | Calcular el volumen de un prisma triangular. | Fórmulas de volumen, cálculo de áreas | Aplicar la fórmula del volumen de un prisma. |
| Teorema de Pitágoras | Calcular la longitud de la hipotenusa de un triángulo rectángulo. | Teorema de Pitágoras | Aplicar el teorema de Pitágoras. |
| Relaciones entre ángulos | Determinar la medida de un ángulo desconocido en un polígono. | Sumatoria de ángulos interiores, ángulos suplementarios | Utilizar las propiedades de los ángulos. |
Recursos Adicionales y Consideraciones Pedagógicas, 20 Actividades Matemáticas Para Desarrollar El Pensamiento Lógico De

La elección del método de enseñanza debe adaptarse al nivel y las necesidades de cada estudiante. Se deben utilizar diferentes recursos y estrategias para mantener la motivación y el interés. El refuerzo positivo es esencial para fomentar la confianza en sí mismos y la perseverancia.
- Métodos de Enseñanza: Se pueden comparar métodos como el aprendizaje basado en problemas, el aprendizaje cooperativo, y el aprendizaje basado en proyectos.
- Recursos Online Gratuitos: Existen numerosas plataformas online que ofrecen actividades matemáticas interactivas y recursos educativos gratuitos.
- Motivación y Refuerzo Positivo: Es fundamental crear un ambiente de aprendizaje positivo y estimulante, donde los estudiantes se sientan apoyados y motivados a aprender.
Ejemplos de Ilustraciones
Las ilustraciones son herramientas esenciales para la comprensión de conceptos matemáticos abstractos. Una buena ilustración debe ser clara, precisa y atractiva visualmente.
Ilustración 1: Juego de Mesa: Una ilustración del juego “La Carrera de las Sumas” mostraría un tablero colorido con casillas numeradas, dados, fichas de colores representando a los jugadores, y una meta claramente definida. Los elementos visuales deben ser atractivos para niños de primaria.
Ilustración 2: Secuencia Numérica Compleja: Una ilustración de una secuencia numérica compleja, como la sucesión de Fibonacci (1, 1, 2, 3, 5, 8…), mostraría una representación visual de la secuencia, con cada número representado por un elemento gráfico (círculos, cuadrados, etc.) de tamaño proporcional al valor del número. Se podrían incluir flechas para mostrar la relación entre los números.
Ilustración 3: Problema Geométrico Complejo: Una ilustración de un problema geométrico que involucre la aplicación del Teorema de Pitágoras mostraría un triángulo rectángulo con sus lados claramente etiquetados. Las etiquetas incluirían las longitudes de los catetos y una incógnita para la hipotenusa. Se incluirían líneas auxiliares para facilitar la comprensión del problema y la aplicación del teorema.
¿Qué edad es la ideal para comenzar con estas actividades?
Las actividades se adaptan a diferentes edades, desde los 6 hasta los 17 años, siendo ajustables según las capacidades del niño o adolescente.
¿Se necesitan materiales especiales para todas las actividades?
No todas las actividades requieren materiales especiales. Muchas utilizan recursos cotidianos o se pueden adaptar a la disponibilidad de recursos.
¿Cómo puedo evaluar el progreso de un niño con estas actividades?
La evaluación debe ser cualitativa, observando el razonamiento y el proceso de resolución de problemas, más que la simple obtención de la respuesta correcta. El enfoque debe estar en el desarrollo del pensamiento lógico.
